[생물정보학 알고리듬 3장] '리드(read)'로부터 유전체 뉴클레오티드 서열 조립하기 :: 드 브루인 그래프, 해밀턴 경로, 오일러 경로

 

 

안녕하세요 TKM입니다!

 

 

 

그동안 영어 공부겸 '생물정보학 알고리듬' 책 내용을 영어로 한 챕터씩 정리해왔는데

 

그러다보니 제가 제대로 내용을 쓰고 있는지, 그리고 제대로 공부가 되고 있는건지 잘 모르겠어서 ㅋㅋㅋ

 

그래서 이젠 영어공부는 다른 걸로 하기로 했고, 책 정리는 익숙한 한글로 하기로 했습니다!

 

 

 

 

책 내용이 인용되는 만큼 만약 문제 되는 부분이 있다면, 아래 메일로 피드백 주시면 조치하도록 하겠습니다 🙏

 

E-mail: tkm1214@naver.com

 

 

유전체 서열을 어떻게 밝힐 수 있을까?

 

 

유전체(genome)를 화학적 방법으로 산산조각내었다고 가정해봅시다! 

 

이때 발생한 작은 DNA 조각을 '리드(read)'라고 하는데, 여기서 겹쳐지는 조각들을 파악해서

 

유전체의 뉴클레오티드 서열을 조립하는 것을 ' DNA 시퀀싱(sequencing)'이라고 합니다.

 

이러한 유전체 시퀀싱을 위한 전통적인 방법은 다음과 같습니다 👏

 

 

 

그렇다면, 위와 같은 방식으로 얻은 '리드'로부터 어떻게 유전체 서열을 파악할 수 있을까요?

 

DNA 시퀀싱을 대략 이해하기 위해 종이에 ACTGACTAGG라고 10개 정도 적은 후에

 

알파벳이 훼손되지 않게 다양한 길이로 조각내 해당 반복서열을 맞춰보기로 했습니다!

 

 

 

물론, 앞서 살펴보았듯 이렇게 미스매치 없이 깔끔하게 동일한 서열로 나오는 경우는 흔치 않겠죠 ㅎㅎ

 

 

 

따라서 책에선 이상적인 상황을 가정해서 모든 리드가 같은 strand에서 왔고

오류 없이 전체 유전체를 완벽히 포괄하며

 

유전체의 모든 가능한 k-mer 길이의 문자열이 리드로 생산되었다는 가정하에 예시를 설명했습니다!

 

저도 그런 가정 하에 유전체 조립 시뮬레이션을 해보도록 하겠습니다 ㅎㅎ

 

 

 

이제 다 조각내었으니 처음에 어떤 서열이었는지 까먹었다고 가정하고 원래 서열을 맞춰봅시다 :)

 

이제 조각들을 원래 ' ACTGACTAGG'로 맞추어볼텐데 먼저 리드 중에서

 

3-mer인 리드들을 찾아서 같은 것끼리 묶어 나열해보았습니다!

 

 

 

ACT, CTA, TAG, CTG, TGA, AGG, GAC 총 7가지 종류의 3-mer가 등장했습니다.

 

제가 유전체 서열을 10개가 아닌 2~3개 정도로 가져왔으면 7가지 종류의 조각이 모두 나오지 못해

 

유전체 조립 순서를 맞추는데 어려움이 있었을 수도 있습니다..! (뒷 글을 읽으시다보면 더욱 동의 되실겁니다)

 

그만큼 정확한 유전체 조립을 위해선 충분한 유전체 양이 필요하지 않을까 싶네요 ㅎㅎ

 

 

1. 유전체 조립 방법: 겹쳐지는 k-mer 연결하기

 

 

유전체 조립을 위해 k-mer들이 k-1개의 글자가 겹쳐지는 경우를 아래와 같은 방식으로 연결합니다.

 

 

 

그렇다면, 어떤 리드를 첫번째로 리드로 하여 유전체 서열 연결을 시작할지 파악하는게 중요할 듯 합니다!

 

 

Q. 서열에서 첫 번째로 오는 3-mer는?

 

이제 유전체 서열에서 첫 번째로 오는 3-mer을 맞추어보고자 하는데

 

만약 3개의 알파벳 중 뒤의 두개가 CT(ex: ACT)인게 하나도 없는 상황에서 앞의 두개가 CT인 3-mer(ex: CTA)가 있으면

 

그것(CTA)이 유전체 서열에서 첫번째로 오는 3-mer일 것입니다.

 

 

 

그렇지만 앞서 조각내서 만들어진 3-mer에 그런 경우가 없어서(ex: ACT, CTA 둘 다 존재)

 

이런 추론으로 첫번째 서열을 찾을 순 없습니다..!

 

참고로, 책에서는 각 k-mer의 첫 k-1 뉴클레오티드와 마지막 k-1개의 뉴클레오티드를 각각 'PREFIX'와 'SUFFIX'라는 용어로 가리키고 있었으며

 

예로, PREFIX(CTA) = CT이고, SUFFIX(ACT) = CT입니다 ✍️

 

허나, SUFFIX(AGG) = GG로 시작하는 PREFIX는 없는 만큼 마지막은 AGG임은 알 수 있겠습니다!

 

 

 

암튼 이제 첫번째 k-mer을 확실히 잡고 연결을 이어갈 순 없다는 걸 이해했으니 방향성 그래프인

 

'겹침 그래프(overlap graph)'를 만들어서 유전체 경로를 찾아봅시다!

 

 

 

 

여기서 동그란 걸 '노드', 화살표를 '에지'라고 하는데 총 7개의 노드와 7개의 에지가 있음을 확인할 수 있습니다!

 

(공부 차 정리하는 거라 내용의 오류가 있을 수 있다는 점 양해부탁드립니다)

 

이 겹침 그래프에서 각 노드가 단 한번씩만 거쳐가게 하는 경로를 찾음으로써 문자열을 재구축할 수 있습니다 :)

 

 

 

 

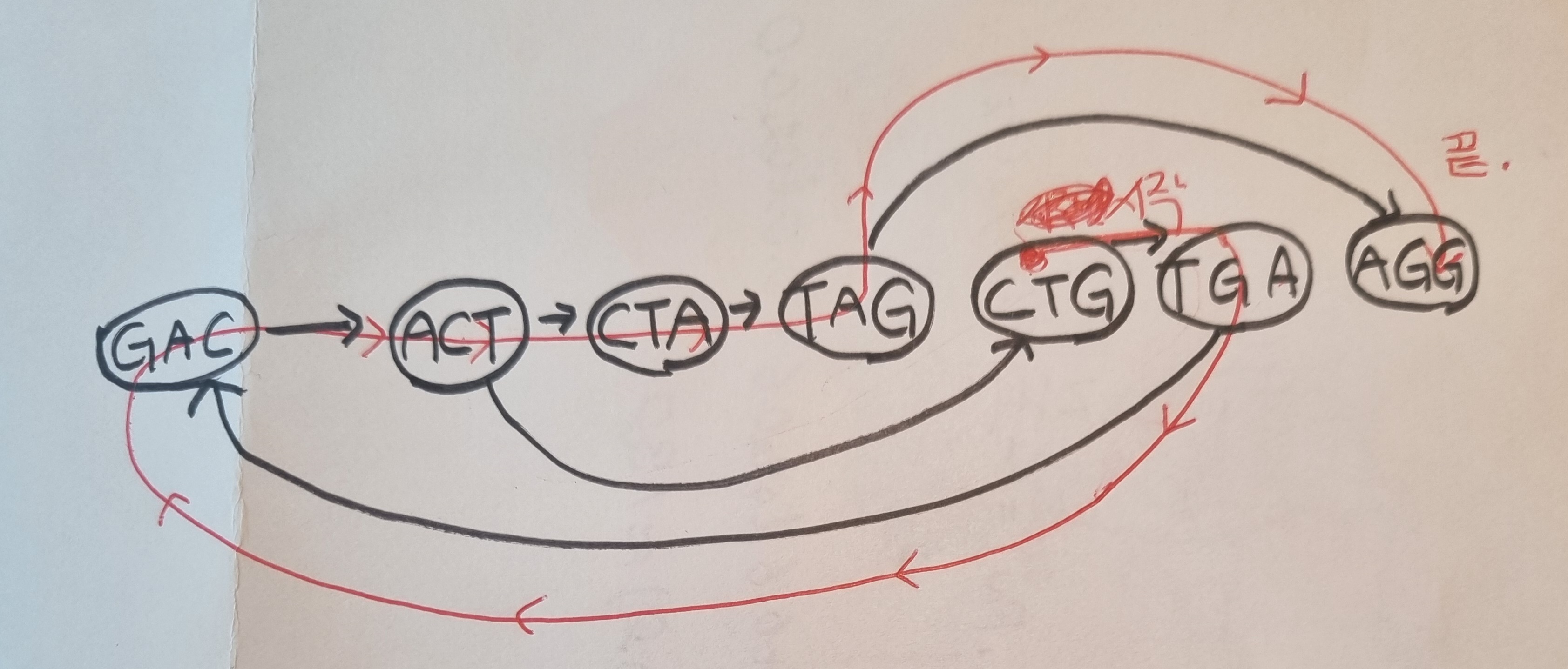
위와 같은 경우 'CTGACTAGG'라는 서열이 만들어지는데

 

실제 서열은 'ACT' 노드를 두번을 거치는 'ACTGACTAGG'라 다르긴 합니다 ㅎㅎ

 

암튼 이처럼 그래프에서 각 노드를 한 번씩만 거치는 경로를 '해밀턴 경로'라고 합니다 👏

 

 

 

그럼 이제 '드 브루인'이라는 사람이 해밀턴 경로를 찾는 대신 

 

k-mer를 표현하는 완전히 다르게 표현하여 만든 '드 브루인 그래프'에 대해 알아보겠습니다 :)

 

드 브루인 그래프를 그리는 방식은 다음과 같습니다!

 

 

 

 

 

 

이런 방식에 따라 앞서 분석하고 있는 예시(3-mer)를 드 브루인 그래프로 나타내면 다음과 같습니다!

 

 

 

 

이 드루인 그래프로 유전체의 뉴클레오티드 서열을 예측해보면 앞서 해밀턴 경로로 예측했던 것처럼

 

다음과 같은 두 가지 서열이 등장하게 됩니다 : CTGACTAGG, ACTGACTAGG

 

 

 

이젠 드 브루인 그래프에서 각 에지를 정확히 한 번만 겹치는 경로를 찾아보려 하는데, 이 경로를 '오일러 경로'라고 합니다.

 

또한, 각 에지를 단 한번만 거치는 거치는 순환 경로를 '오일러 순환 경로',

 

그런 순환 경로를 갖고 있는 그래프를 '오일러식'이라고 합니다!

 

 

눈치채셨겠지만, 제가 예시로 그린 드 브루인 그래프는 들어오는 에지의 수와 나가는 에지의 수(ex: 노드 CT)가 다른 부분이 있기에

 

균형을 이루었다고 보기 어렵고 그렇기에 '오일러 식'이 되지 못합니다..!

 

 

 

 

그 외에도 균형을 이루기 위해선 필요한 조건이 있습니다 👏

 

 

 

아래는 책에 나온 예시를 똑같이 그려봤는데, 해당 조건에 따라 왼쪽은 균형은 이뤘지만 오일러 그래프가 되지 못하고(강력하게 연결 X)

 

오른쪽은 균형을 이루었으면서 오일러 그래프 (강력하게 연결 O)가 됩니다 ㅎㅎ

 

 

 

다음 장에선 드 브루인 그래프의 한계에 대해 알아보며 3장을 마무리 해봅시다 👏

 

 

Bioinformatics OPEN STUDY | Notion

 

 

과학 is 일상 : 네이버 블로그