안녕하세요, 이번엔 최근에 완독한 '딥러닝을 위한 수학' 책을 정리해보려고 합니다.

본 책은 수학책이면서 수학을 프로그래밍으로 구현하며 여러 심층학습 개념들을 소개해주는 게 좋았는데요. 물론 기본을 다룬 책이긴 하지만, 저에겐 꽤 어렵더군요. 수학은 역시 쉽지 않은 것 같습니다.
우선 딥러닝(심층학습)이란 무엇일까요? 딥러닝은 '인공신경망'을 기반으로 데이터로부터 특징을 추출하고, 특징 간의 패턴을 학습하여 판단 및 예측하는 기술이라고 볼 수 있습니다. 이는 특징이 주어지면 그로부터 패턴을 학습하여 판단 및 예측하는 고전적인 머신러닝과는 차이가 있죠.
그렇다면 '인공신경망'은 무엇일까요? ANN(Artificial Neural Network)라고도 불리는 '인공 신경망'은 인간의 뇌와 유사한 계층 구조의 상호연결된 노드(또는 뉴런)을 사용하여 학습하는 적응형 시스템 1)으로 정의됩니다. 즉, 여러 노드들이 인공신경망을 구성하며, 각 노드엔 하나 이상의 연결이 입력되고, 노드로부터 하나 이상의 연결이 출력됩니다. 그리고 이러한 노드들의 연결 강도를 다양하게 변화시킴으로써 어려운 계산을 해낼 수 있는 복잡성을 얻을 수 있습니다 2). 참고로, 뉴런들이 모여 형성된 심층 신경 네트워크(DNNs, deep neural networks)에서 '심층(deep)'은 다수의 층으로 구성된 네트워크 구조(multilayer network structure)를 묘사한다4)고 하는데요. 간단한 딥러닝의 모식도는 다음과 같이 '입력층', '숨겨진 층', '출력층'으로 구성됩니다.

개념에 대해 소개했다면, 이제 책 내용을 간단하게 정리해보겠습니다. 자세하고 정확한 내용은 '딥러닝을 위한 수학' 책을 읽어보시길 추천드립니다.

본 책에서는 여느 프로그래밍 책처럼 우선 실습을 위한 환경 설정 방법을 소개한 뒤, 수학 책 답게 '확률'에 대한 이론적인 개념부터 친절하게 소개해주고 있었습니다.
로또에 당첨될 확률은 어느 정도일까요? 챗GPT에게 물어봤습니다.

물론, 보너스 점수라는 개념이 한국 로또엔 있긴 하지만, 그래도 1등이 되는 건 여전히 어려울 듯 합니다. 이처럼 어떤 일이 일어날 가능성 0과 1사이의 숫자로 나타낸 것을 '확률'이라고 합니다. 저자가 말하길, 확률을 다룰 땐 주어진 사건의 모든 가능한 결과를 하나의 표본 공간(sample space)으로 묶어서 취급한다고 하는데요. 이러한 표본 공간은 셀 수 있는 이산 집합일 수도 있고, 셀 수 없는 연속 구간일 수도 있습니다. 이산 집합의 예로는 '로또 번호', 연속 구간의 예로는 '몸무게'가 있습니다. 그리고 표본 공간 내에서의 개별 사건은 표본 공간의 부분 집합으로서 '표본(sample)'이라고 표현합니다.
딥러닝과 머신러닝에 자주 등장하는 확률 개념은 '확률 분포 및 표본 추출(표집)'과 '베이즈 정리'라고 합니다. 저자는 확률 분포에 대해 다음과 같이 설명합니다.
확률 분포(probability distribution)를 요구에 따라 값들을 생성하는 함수라고 생각해도 될 것이다. 그 값들은 무작위로 생성된다. 즉, 어떤 값들이 나올지는 미리 알 수 없다. 그러나 각 값이 생성될 가능성은 주어진 확률 분포가 정의하는 특정한 패턴을 따른다. 3)
이러한 확률분포는 딥러닝에서 훈련 이전 신경망을 초기화하는데 사용할 값을 마련하기 위해 사용된다고 하는데요. 뒤에서 설명하겠지만, 딥러닝에서는 신경망에서의 가중치와 치우침항 값들을 초기값으로부터 역전파와 경사하강법을 통해 갱신해나가며 예측 성능을 높입니다. 마치 K-평균 클러스터링에서 임의의 k 개의 중심점을 랜덤하게 정하고, 그 점으로부터 가까운 것(유사도 기준)끼리 묶은 뒤, 묶은 것끼리 평균을 계산해서 점점 비슷한 것끼리 묶이도록 하는 방식과 유사한 듯 합니다. 책에서는 먼저 확률 분포(이산확률분포, 연속확률분포)의 종류와 각각에 대한 개념을 소개해줍니다.
이번엔 또 다른 주요 개념인 베이즈 정리에 대해 소개하겠습니다. 베이즈 정리의 국어사전 정의 4)는 '주어진 조건에서 어떠한 현상이 실제로 일어날 확률을 구하는 방법'인데요. 정의만 봤을 때 추상적이면서 어떻게 실제 확률을 구하는 것인지 궁금증이 생길 듯 합니다. 쉽게 말하면, 어떤 현상의 확률을 예측할 때 새롭게 얻은 정보를 바탕으로 기존 예측(사전확률)을 업데이트해 예측 정확도를 높이는 방법이 베이즈 정리입니다. 베이즈 정리를 활용하는 대표적인 예시로는 '단순 베이즈(Naive Bayes) 분류자'라는 기법이 있습니다. 이는 어떤 데이터(특징 벡터 x)가 주어졌을 때 그것이 특정 분류명 y에 속할 확률 P(y|x)를 계산해주는 알고리즘입니다.

예로, 이메일이 왔을 때 그 이메일이 스팸일 확률과 스팸이 아닐 확률을 각각 계산해서 더 높은 확률 쪽으로 분류를 한다고 해봅시다(챗GPT의 예이지만, 실제로 스팸 분류에 베이즈 분류가 효과적인 성과를 냈다고 알려져 있습니다). 여기서 분류명 y는 '스팸' 또는 '정상 메일'이 될 것이고, 특징 벡터 x는 이메일 본문에 포함된 단어들, 발신인 정보, 제목에 사용된 표현 등이 될 수 있습니다. 단순 베이즈 분류자는 "이메일의 모든 특징(단어, 발신 등)이 주어졌을 때 스팸이 될 확률 P(스팸 | 특징 x)는 얼마인가?"를 계산하는 방식으로 작동합니다. 이러한 확률을 구하면, 실제로 새 이메일이 들어왔을 때 각 분류명에 대한 확률 중 가장 높은 값을 가진 쪽으로 최종 분류를 결정할 수 있습니다. 예로, P(스팸|x)가 P(스팸|x)보다 크면 그러한 특징 벡터 x를 가진 메일을 스팸으로 분류하는 식입니다. 베이즈 정리를 식으로 나타내면 다음과 같습니다.
P(y|x) = P(x|y) * (Py) / P(x)
다음으론 저자는 '통계'의 개념에 대해 소개합니다.
통계량(statistic)은 어떠한 표본에서 계산한, 그리고 그 표본을 어떠한 방식으로 특징짓는 수치이다. 일반적으로 심층학습에서는 데이터 집합이 표본에 해당한다 3).
저자가 말하길, 새로운 데이터 집합을 마련했을 때 가장 먼저해야 할 일은 바로 적절한 요약 통계량을 계산하는 것이라고 합니다. 그리고 두 데이터 집합이 같은 모분포에서 비롯된 것인지 알고자 할 때 기본적으로 할 만한 일은 '요약 통계량'을 살펴보는 것이라고 합니다. 가장 기본적인 통계량은 데이터 집합을 단 하나의 수치로 요약한 '평균'이죠. 참고로, 평균 중에는 데이터 집합 요소 중 중요한 것과 덜 중요한 것을 구분해 서로 다른 가중치를 부여(각 값에 1/n의 가중치가 부여)하는 가중평균이 있습니다. 평균 외에도 다양한 통계량이 '표본'이라는 데이터 집합을 특징지을 수 있습니다. 그중 '분산'이라는 통계량이 머신러닝과 딥러닝에 자주 활용되는 것 같습니다. 단순 추측일 뿐 아닐 수도 있습니다. 중요한 것은 우리가 데이터 분석에서 사용하는 것은 대부분 '전체'가 아닌 '전체'를 묘사한다고 믿는 '전체의 일부'라는 것입니다.
우리는 진(true) 모분산 값과 진 모평균 값을 알지 못한다. 그저, 우리가 가지고 있는 데이터 집합에서 그 둘을 표본의 평균과 분산으로부터 추정할 뿐이다. 따라서 편향 표본 분산 값은 편향되었으며, 모분산에 대한 최선의 추정치가 아니라는 점과 베셀 보정을 가하면 모분산을 좀 더 잘 추정할 수 있다는 주장이 널리 받아들여지고 있다. 3)
여기서 베셀 보정은 비편향 표본 분산을 계산할 때, 편향 표본 분산과 달리 표본의 개수 전체 n으로 나눠주는 것이 아닌 n-1로 나눠주는 것을 말하는데요. 이는 표본 내의 값들이 표본 평균에 가깝게 모이는 경향이 있어서 표본 자체에서 평균을 뽑아오면 전체 모집단의 평균과 비교했을 때 덜 퍼져 보이는 효과(과소 추정 효과)가 발생하기 때문입니다. 즉 표본을 기반으로 분산을 계산하면, 실제 모집단의 분산보다 작은 값을 얻게 되기에 이를 보정하기 위해 n이 아닌 n-1로 나누는 방식을 사용한다고 합니다. 물론, 심층학습에 흔히 쓰이는 대형 데이터 집합에선 편향 표본 분산으로 하든 비편향 표본 분산으로 하든 별 차이가 없다고 하죠. 참고로, 표본 평균들의 표준편차는 '표준 오차'라고 합니다.
Seurat으로 scRNA-seq 분석 과정에서 바이올릿 플롯을 그릴 때 박스 플롯을 같이 그리면 좋다고 하더군요. 본 책에서 박스 플롯에 대한 설명도 해주어서 좋았습니다.
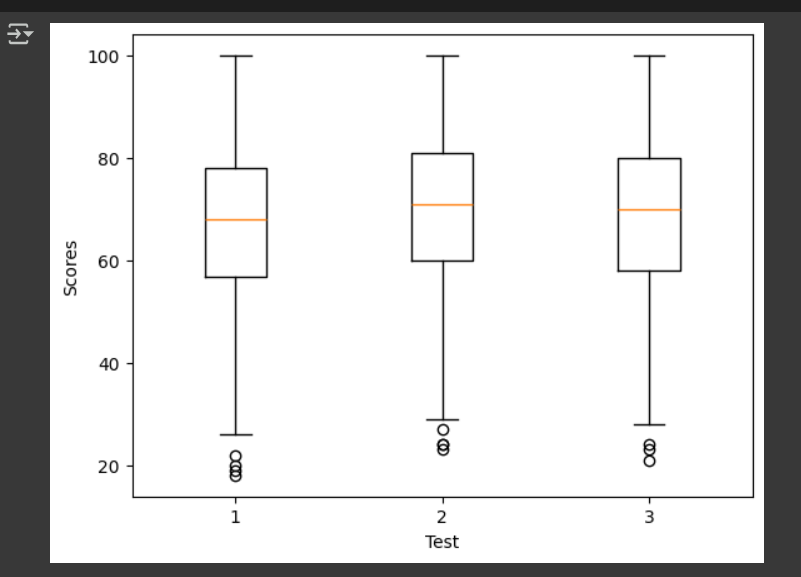
박스 플롯에서의 '박스'는 일반적으로 1사분위수(Q1)와 3사분위수(Q3)의 위치를 표시하며(Q3과 Q1의 차이는 사분범위(interquartile range, IQR)라고 부름), 여기서 분위수(quantile)는 데이터 집합을 고정된 크기의 여러 분위로 나누는 값3)이라고 볼 수 있습니다. 상자 중간에 있는 선은 중앙값(Q2)이고, 상자 위아래 뻗어나온 선들은 수염(whisker) 혹은 플라이어(flier)라고 부르며, 수염 바깥의 값들은 잠재적 이상치로 볼 수 있다고 합니다. 잠재적 이상치는 이상치가 아닐 수 있습니다. 어쩌면 어떤 가치있는 인사이트를 제공하는, 특정 특징을 잘 나타내는 데이터일수도 있죠. 이것이 시퀀싱 데이터를 전처리할 때 까다로운 이유 중 하나가 아닐까 싶습니다. 우리는 통계를 가지고 실제값을 예측할 뿐, 그것이 정말로 맞는지 모를 수 있으니까요. 그래도 우리의 세계에서 표본이 충분히 많으면 예측할 수 있는 값이나 일정한 패턴(ex. 정규분포)이 나타나게 된다는 건 참 다행인 것 같습니다.
암튼 이상치 외에도 신경써야 할것으로는 있어야 하는데 없는 데이터인 결측 자료(missing data)가 있습니다. 이런 결측자료는 특정한 방식으로 부호화하곤 합니다. 예로 유효한 값이 항상 양수라면 결측 특징은 -1로 표시하기도 하고, 문자열로 표현되는 특징이라면 빈 문자열을 결측값 표시 용도로 사용할 수 있다고 합니다. 또한, 특징들의 평균으로 결측값을 대신하기도 하는데요. 만약 특징들의 분포가 정규 분포가 아니라면, 평균보다 이상치와 극단치에 덜 민감한 중앙값을 사용하는 게 더 나은 대안일 수 있다고 합니다. 이때, 정규분포인지 아닌지는 요약통계량, 상자그림, 히스토그램 등으로 확인할 수 있습니다.
다음으로 소개한 개념은 '상관관계'입니다. 상관관계는 한 특징이 증가하면 다른 어떤 특징이 증가하는 관계(꼭 정비례는 아니어도 ok) 혹은 한 특징이 올라가면 다른 특징이 내려가는 관계를 나타냅니다. 이렇듯 두 특징이 얼마나 강하게 연관되는지, 상관계수의 수치를 표현하는 방법에는 대표적인 방법 두 가지가 있습니다. 첫번째는 '피어슨 상관계수(Pearson correlation coefficient)'입니다. 피어슨 상관계수는 두 특징 사이의 선형 상관관계의 세기이자 [-1, +1] 구간의 값으로(보통 r로 표기), 여기서 '선형'은 "두 특징의 상관관계가 얼마나 강한지를 하나의 직선으로 서술할 수 있다는 의미" 3)라고 합니다. 또 다른 상관계수로는 스피어먼 상관계수가 있습니다. 이 상관계수도 [-1, +1] 구간의 값이며 ρ로 표기하지만, 특징 값들 자체가 아닌 특징 값들의 순위에 기초한다는 점에서 차이가 있습니다. 따라서 스피어먼 상관관계 방식은 인수 사이의 비선형 관계를 반영할 수 있다는 장점이 있습니다(구체적인 수치가 아니라 순위로 상관성을 판단하기 때문).
가설 검정에서는 두 종류의 가설을 사용한다. 하나는 두 데이터 집합이 사실은 같은 모집단에서 나왔을 것이라는, 다시 말해 우리가 의심하는 바가 틀렸을 것이라고 가정하는 가설이다. 이를 귀무가설 또는 영가설(null hypothesis)이라고 부르고 H0으로 표기한다. 다른 하나는 두 그룹이 같은 모집단에서 나온 것이 아니라는 대안가설(alternative hypothesis)이다. 3)
참고로, 가설검정은 귀무가설이 진짜인지 아닌지 말해준 게 아닌, 단지 확률적으로 봤을 때 이 귀무가설을 기각할 수 있을지, 승인할 수 일지 판단하는데 사용할 근거를 제시하는 정도라는 걸 기억하는 것이 중요하다고 합니다. 그 근거로 사용되는 것이 p값인데, p값에 대해선 뒤에서 설명하도록 하겠습니다. 이러한 가설 검정은 결국 독립적인 두 표본이 같은 모집단에서 비롯된 것인지 파악하는 데 활용되는데요. 이를 통해 두 데이터 집합의 평균들에 유의미한 차이가 존재하는지 우리는 알고 싶어 합니다. 차이가 존재한다는 것은 한 쪽이 다른쪽보다 클 수도 있고 작을 수도 있다는 의미입니다. 이럴 때 활용하는 검정을 '양면 검정(two-side)'이라고 하며, 대표적인 양면 검정에는 't-검정'이 있습니다.
t-검정은 모수적 검정으로, 데이터가 '동일 독립 분포'이면서 데이터의 분포가 '정규분포'라고 가정합니다. 그리고 t-검정 중 하나인 '웰치의 t 검정(Welch's t-test)'은 두 집단의 분산이 동일하다고 가정하지 않는 '독립 표본 t-검정의 변형'입니다. 그렇게 t-점수들로 규정되는 t-분포 곡선의 특정 구간에서 곡선 아래의 면적을 계산해서 p-값을 구한다고 하는데요. p값하면 왠지 모르게 '0.05 미만'이 떠오르게 됩니다. 작을 수록 좋다는 건 알겠는데, 왜 작을수록 좋을까요? 그 이유는 여기서 p값이 귀무가설이 참이라는 것을 전제로 하기 때문입니다. 우리가 원하는 건 귀무가설을 기각하여, 통계적으로 유의미한 차이가 존재하다는 결과를 얻고 싶은데 말이죠. 물론, 유의한 차이가 없다는 것도 유의한 결과 일 수 있을 것입니다.
구체적으로, p값은 '만일 귀무가설이 참이라면, 두 평균이 다를 확률'이라고 합니다. 즉, 두 집단이 동일한 모집단에서 왔을 때 두 평균이 다를 확률이라는 의미로, p값이 높다면 두 집단은 동일한 모집단에서 왔다는 의미이겠죠. 일반적으로 이 확률이 우리가 정한 어떤 값(ex. 0.05)보다 작으면 두 그룹이 서로 다른 모집단 분포에서 비롯했다는 증거로 간주합니다. 물론, 앞서 말했듯 그저 추정이기에 정확한 결과가 아닐 수 있으며, 이를 보정하기 위해 FDR(False Discovery Rate)을 반영한 adjusted P value를 사용하기도 합니다. 심지어 통계적으로 유의한 p값이 나왓어도 그 효과는 의미가 없을 수 있습니다. 이것이 '효과 크기(effect size)'를 측정해야 하는 이유이죠. 효과 크기를 계산할 땐 '코헨의 d 공식'이 사용되곤 하는데, 이는 두 그룹 간 평균 차이를 활용하기에, 차이의 크기를 나타냄에 있어 유용한 지표가 됩니다.
t-검정 외에 원본 데이터가 정규분포가 아닐 때 사용하는 비모수적 검정으로, '맨-휘트니 U 검정(윌콕슨 순위합 검정)'이 있습니다. 맨-휘트니 U 검정은 앞서 스피어먼 상관계수처럼 데이터 값들 자체가 아닌 데이터 값들의 순위(rank)를 사용합니다. 이 검정의 귀무가설은 t-검정과 살짝 다른데, '그룹1에서 무작위로 선택한 값이 그룹2에서 무작위로 선택한 값보다 클 확률은 0.5이다'가 귀무가설이라고 합니다. 만약 두 그룹이 동일한 모집단에서 왔다면 한 그룹이 다른 그룹보다 선택한 값이 클 확률은 0.5로 수렴하겠죠. 반대로, 만약 클 확률이 0.5보다 크거나 작으면 이는 두 집단이 서로 다른 모분포에서 비롯되었다는 증거로 간주할 수 있습니다. 결국 맨-휘트 U 검정은 t-검정과 달리 평균들의 차이가 0인지 묻는 건 아니지만, 두 집단이 실제로 서로 다른 모분포에 비롯했다면 귀무가설을 기각한다는 점에서 동일합니다.
다음으로 '선형 대수'를 1부와 2부로 나누어서 소개해줍니다. 선형대수의 정의에 대해 챗GPT에게 물어봤습니다. 챗GPT는 선형대수를 수학의 한 분야로서, 벡터, 행렬, 그리고 이들이 속한 선형공간(또는 벡터 공간)과 이 공간 위에서의 선형변환을 다루는 분야로 소개했습니다. 저자가 말하길, 심층학습 알고리즘을 구현하는 프로그램은 데이터를 벡터나 행렬 같은 객체로 취급해서 '선형대수'를 적용한다고 하는데요. 저자께서 내용을 최대한 쉽게 적어주시긴 했지만 역시 수학은 어렵습니다. 그래도 심층학습에서 활용되는 선형대수 개념들에 대해 슬쩍 알아갈 수 있는 기회가 되었습니다. 오랜만에 기하와벡터에서 배웠던 '외적'과 '내적'에 대해 복습도 해보고(사실 그때 기하와벡터에서 외적과 내적을 배웠는지 기억이 가물가물하긴 합니다), 행렬곱셈, 행렬식 구하기 등등 여러가지 수학 공부를 했습니다. 중요한 것은 선형대수가 딥러닝에 적용된다는 것이죠. 구체적으로, 딥러닝의 노드에서는 입력 벡터에 대해 가중치 행렬과 치우침 벡터를 적용해서 새 벡터를 출력합니다.
순방향 신경망(feedforward neural network)은 입력에 상관변환들을 차례로 적용하는 것이라고 할 수 있는데, 이때 신경망 층들 사이의 가중치 행렬이 변환 행렬이고 치우침 벡터가 이동 벡터이다. 이것만으로는 층들이 선형 관계를 가지지만, 각 층의 활성화 함수 때문에 비선형 관계가 생긴다. 이러한 비선형성 덕분에, 신경망은 입력을 적절한 함수 관계(신경망 설계 시 의도한)가 반영된 출력으로 사상하는 새로운 방법을 배우게 된다. 3)
심층학습에서는 '두 벡터의 거리'를 노름(norm)이라고 부를 때가 많다고 하는데요. 벡터 x와 벡터 y의 거리는 그 둘의 차이에 해당하는 벡터의 노름이라고 합니다. 이때, 벡터의 내적을 한 뒤(성분별로 차이를 제곱한 값을 합한뒤), 거기에 제곱근을 붙인 'L-2 노름'은 두 벡터의 유클리드 거리로 활용됩니다. 참고로, 노름 식은 다음과 같이 정의되며, L-2 노름은 p에 2를 넣은 것이고, 1을 넣은 L-1 노름은 '맨허튼 거리'라고 부른다고 합니다.

L2 노름인 유클리디안 거리는 scRNA-seq 데이터 분석에서 고차원 유전자 발현 프로파일을 비교하는 데 활용됩니다. 구체적으로, 차원 축소 후 계층적 클러스터링을 진행할 때 유클리디안 거리를 활용해 유사한 세포들을 순차적으로 병합하거나 분할하여 계층 구조의 클러스터를 형성할 수 있습니다. 거리가 짧을수록 유사한 전사체적 특징을 가진 세포이고, 같은 세포 유형일 가능성이 높으니까요. 이외에도 L-2 노름은 딥러닝에 있어서 가중치가 너무 커지지 않게 하는 '가중치 감쇠(weight decay)'를 위한 정칙화항으로도 활용될 수 있다고 합니다.
마할로노비스의 거리는 좌표상의 거리를 측정하는 '유클리디안 거리'와 달리, 데이터의 스케일 차이와 변수 간의 상관관계를 보여주는 거리이자, 데이터 벡터 x가 평균 벡터 μ에서 얼마나 멀리 떨어져 있는지를 공분산을 고려하여 측정하는 거리 3)라고 합니다. 여기서 '공분산'은 두 확률변수 간의 관계를 나타내는 측도로, 만약 공분산이 양수면 두 변수는 같은 방향으로 움직이는 경향이 있고, 음수면 반대 방향으로 움직이는 경향이 있으며, 0에 가까우면 서로 독립적이거나 선형 관계가 약함을 의미한다 5)고 합니다.

마할라노비스 거리를 이용해서 간단한 분류자(classifier)를 만들 수 있다. 각 특징 벡터에 여러 분류명 중 하나가 배정된 데이터 집합이 있다고 하자. 목표는 미지의 특징 벡터 x가 어떤 분류명에 속하는지를 결정하는 것이다. 이를 위해 먼저 분류명마다 평균 벡터를 계산해둔다(이 평균 벡터를 무게중심(centroid, 또는 중심) 벡터라고 부르기도 한다). 그런 다음 미지의 특징 벡터와 각 분류명 무게중심과의 마할로비스 거리를 구한다. 그 거리 중 가장 작은 것에 해당하는 분류명이 미지의 특징 벡터의 분류명이다. 3)
또 짚고 넘어가지 않을 수 없는 개념도 소개가 되었는데요. 바로 '주성분 분석'입니다. 저자는 주성분 분석에 대해 데이터가 주로 어느 방향으로 흩어져 있는지 파악하는 방법이라고 설명합니다. 보통 주성분 분석하면 '차원 축소'가 떠오르지만, 차원축소는 주성분 분석 결과를 활용하는 방법으로 보는 것이 맞을 듯합니다.
주성분은 보통 분산이 가장 큰 방향을 가리키는데요. 분산이 가장 큰 방향으로 선을 긋게 되면 그 선은 오차를 최소화하며 데이터를 잘 대표하게 됩니다. 그렇게 주성분 분석은 먼저 주성분을 구한 뒤, 분산이 감소하는 순으로 나머지 성분들을 구합니다. 이때 중요한 특징이 각각의 새 성분은 이전의 모든 성분과 수직이라는 것입니다. 그 이유가 궁금해서 실수할 수 있지만 그래도 저보다 실수할 가능성이 낮은, 그래서 참고하기 좋은 챗GPT에게 물어봤습니다. 그가 말하길 새성분이 이전 성분의 수직인 이유는 중복 없는, 즉 독립적인 정보 추출을 보장하기 위해서라고 볼 수 있다고 합니다. 즉, n+1번째 주성분에서 n번째 주성분이 설명한 정보를 중복해서 포함하지 않도록 하기 위함이라고 볼 수 있겠습니다.
주성분 분석은 데이터 집합의 차원을 줄이는 용도로 흔히 쓰인다. 관측값이 변수 100개로 구성되며, 처음 두 성분이 전체 데이터 산포의 95%를 설명한다고 가정하자. 데이터 집합을 그 두 성분을 따라 사상하고 나머지 98개의 성분을 폐기하면, 단 두 개의 변수로도 데이터 집합을 적당히 특징지을 수 있다. 즉, 100차원을 2차원으로 축소하는 것이다. 반대로, 주성분 분석으로 데이터 집합을 증강(augmentation)할 수도 있다(특징들이 연속값일 때). 3)
본 책의 미분, 역전파, 경사하강법에 대한 정리는 다음 글에서 해보도록 하겠습니다. 감사합니다!
참고자료
1) MATLAB, URL : https://kr.mathworks.com/discovery/neural-network.html
2) 이용석 외 5명, 생물정보학 입문, 월드 사이언스, 2024
3) 로널드 크노이젤 저/류광 역, 딥러닝을 위한 수학, 제이펍, 2022
4) 네이버 국어사전, 베이즈 정리
5) 위키독스, 공분산의 성질, URL : https://wikidocs.net/256585



