오늘은 8일차에 정리한 mendelian randomization analysis 중 하나인 two-sample MR에 대해 분석 기법과 함께 소개해보도록 하겠습니다.
[대학원 준비 8일차] MR analysis (mendelian randomization analysis)에 대하여
이번 글에선 전 글에서 살펴본 SNPs를 사용하는 Mendelian randomization(MR) analysis에 대해 알아보겠습니다. What is Mendelian Randomization(MR)? MR에 대한 간단한 설명은 아래 영상을 확인해보시면 되겠습니
tkmstudy.tistory.com
우선 two-samle MR은 risk factor(exposure)와 outcome을 위한 두 가지 study samples를 사용하여
risk factor의 ourcome에 대한 cause effects를 평가하는 방법으로,
different sources로부터 유래된 genotype data를 통합하여 combine effects를 측정할 수 있다1)고 합니다.
아래는 TwoSample MR에 대해 설명하는 유튜브 영상입니다.
MR analysis를 위해 측정되는 방법으로는 inverse variance weighted(IVW), MR-egger 등이 있는데요,
genetic variants의 casual efftects를 검출하기 위해 사용하는 주요 MR method는 IVW이고,
다른 방법은 IVW의 결과의 설명력을 보충하거나, 검증하기 위해 사용됩니다 1).

기본적으로 exposure(X)의 outcome(Y)에 대한 causative effect를 계산하는 쉬운 방법은 Wald ratio를 활용하는 것인데
Wald ratio는 'βZY(outcome) / βXY(exposure)'로 계산하며, 여기서 β는 effect size를 의미합니다.
즉, outcome에 대한 genetic variant의 effect size를 exposure에 대한 genetic variant의 effect size로 나눈 비율로 볼 수 있습니다.

여기서 effect size는 variables 사이의 relatinoship 혹은 두 그룹 사이의 차이가 얼마나 유의미한지 알려주는 척도로 large effect size는 research finding이 통계적으로 유의미하다는 것을 말합니다.
effect size를 계산하기 위해서는 보통 Cohen's d와 Pearson's r을 사용하는데, Cohen's d는 두 그룹 사이의 차이의 size를 알려주고 Pearson' r은 두 변수들 사이의 관계가 얼마나 strong한지를 측정합니다 3).
더 자세한 설명은 하이퍼링크의 'How do you calculate effect size?' 관련 글을 참고하시면 됩니다.
지금 하는 건 두 변수 간의 관계를 평가하는 것인 만큼 effect size 계산에 pearson correlation이 활용될텐데, 이에 대한 설명 영상을 아래에 첨부합니다.
IVW는 여러 genetic variants가 특정 exposure와 관련이 있을 때 각 variant의 specific Wald ratios의 meta-analysis*를 통해 계산합니다.
* meta-analysis : multple independent studies로부터의 정보들을 pooling하는 tool 2)
챗GPT에게 IVW estimate를 어떻게 계산하는지 물어봤더니 다음과 같이 알려줬습니다.

여기서 wi 계산에 쓰이는 'inverse variance weight'는 SE(i)^-2로 계산합니다.
SE(standard error)는 표준 오차로, 이렇게 계산하는건 wi를 true variance로서 고려하기 위한 common practice라고 합니다 2).
수식은 직관적으로 이해되지 않으니 그냥 그렇구나 하고 넘어가도록 하겠습니다.
결국 중요한건, 똑똑하신 분들이 만든 수식으로 IVW estimation을 하면, LD(linkage disequilibrium)에 있는 genetic variants의 pair를 제거하여 정확도를 높일 수 있고 1), 무엇보다 genetic variant의 casual effect의 weighted average를 구할 수 있습니다 3).
여기서 왜 ‘inverse variance weighting(IVW)이냐 하면 본 측정법에서 각 casual SNP's effect가 ratio estimator의 variance의 inverse에 의해 weighted되기 때문입니다.
무슨 말인지 저도 적어놓고 무엇인지 몰라서 챗GPT에게 쉽게 설명해달라고 요청해봤습니다.

암튼 그렇게 inverse of variance로 정확도를 높여 overall causual effect를 weighted SNP casual effects의 합으로 계산하기 때문에 그런 이름으로 정했다고 합니다 4).
따라서 IVW를 활용해서 exposure의 outcome에 대한 casual effect가 있는지 결과값으로 도출된 p값을 통해(p < 0.05) 유의미한지 확인하고,
odds ratio(OR > 1 : positive correlation, OR = 1 : no association OR < 1 : negative correlation)를 통해 상관관계의 방향을 확인할 수 있습니다 5).
odds ratio에 대한 이해를 돕기 위해 아래에 유튜브 영상 링크를 첨부합니다.
IVW 계산하는 예시를 들기 위해 Two sample MR을 수행할 수 있는 MR base 사이트에서 exposure을 특정 장내 미생물, outcome을 Alcheimer's Dises로 두고 상관관계 분석을 해보았습니다.
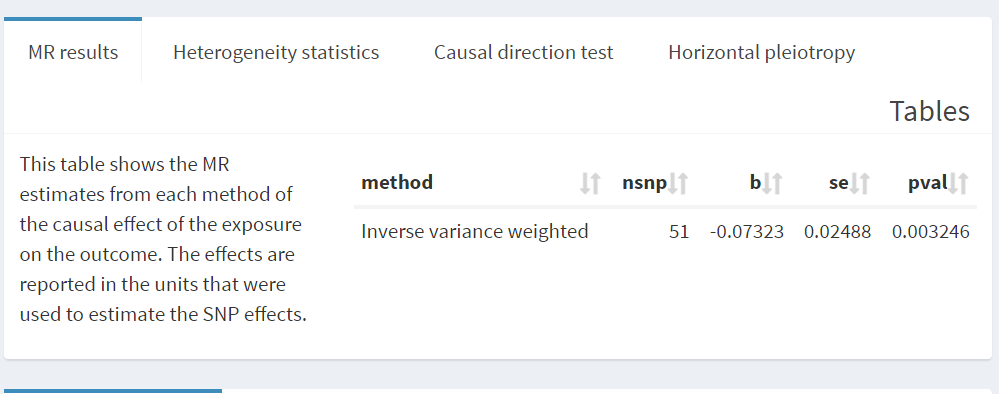
결과적으로 p value가 0.05 미만으로 유의미하고, beta는 odds ratio로 변환해서 계산할 수 있는데 e^beta가 odds ratio입니다.
beta가 -0.07323이니까 변환해서 계산하면, odds ratio는 0.92939 정도 나오고, 그러면 특정 장내미생물과 AD 사이의 관계가 negative correlation인 것으로 알 수 있습니다.
SNP의 수(snps)도 적당하고, se(standard error)도 너무 크지 않으니까요.
그렇지만, MR 계산에 있어서 IV assumption의 세 번째던, genetic variant가 오직 exposure을 통해서만 outcome에 영향을주는지 즉, pleiotropy(다면 발현성) 없는지 확인하기 위해 MR-Egger regression 분석도 진행을 해주어야 합니다.
MR-egger regression을 사용하면 exposue-outcome casual association의 horizontal pleiotropy의 규모를 측정할 수 있는데,
만약 pleiotropy가 발견되지 않는다면 intruments가 exposure가 아닌 다른 pathways로 outcome에 영향을 주지 않는다고 할 수 있고,
그러려면 MR-egger regression 계산에서 p 값이 0.05보다 작아선 안될 것(p값이 0.05라면 intercept가 0이 아니어선 안될 것)입니다(유의해선 안될 것입니다).
다시 말해, MR-Egger은 GWAS summary statics에서 two-sample MR studies에서 horizontal pleitoryp로부터 유래된 bias가 있는 확인 4)하는데 사용됩니다.
앞서 분석했던 장내미생물과 AD 사이의 상관관계 분석에서 horizontal pleiotropy를 확인하니 p-value가 0.05 이상이니 pleiotropy가 영향을 주지 않았다고 할 수 있겠습니다.
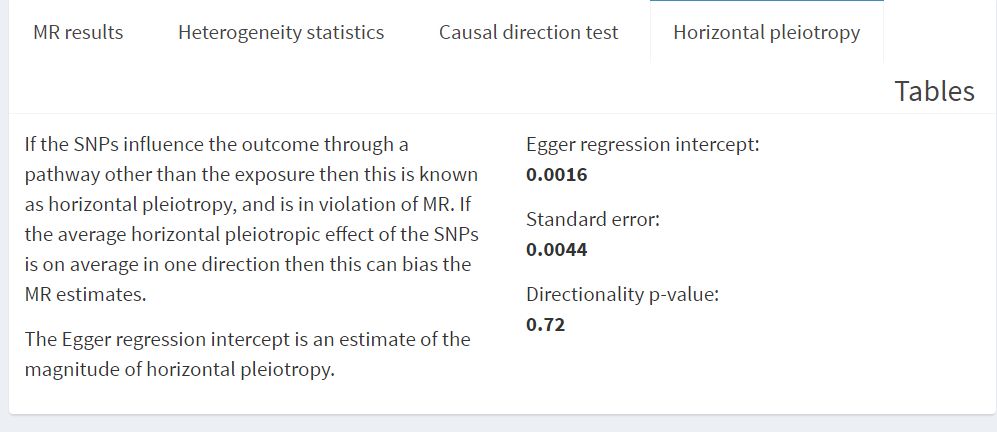
아래 영상에선 Egger's regression에 대해 설명해주는데 7분 21초부터 재생속도 1.5배로 보시길 추천드립니다.
이렇게 IVW, MR-egger regression 등으로 파악한 casual effect estimates가 정말 믿을 만한지 한번 더 알아볼 수 있게 sensitivity analysis로 'leave-one out analysis'를 수행할 수도 있는데
본 분석 방식은 MR estimate가 single SNP(outliers)에 의해 결과가 왜곡되는 것은 아닌지 SNP를 하나씩 순차적으로 떨어뜨려서 effect를 재평가하는 방식입니다 6).
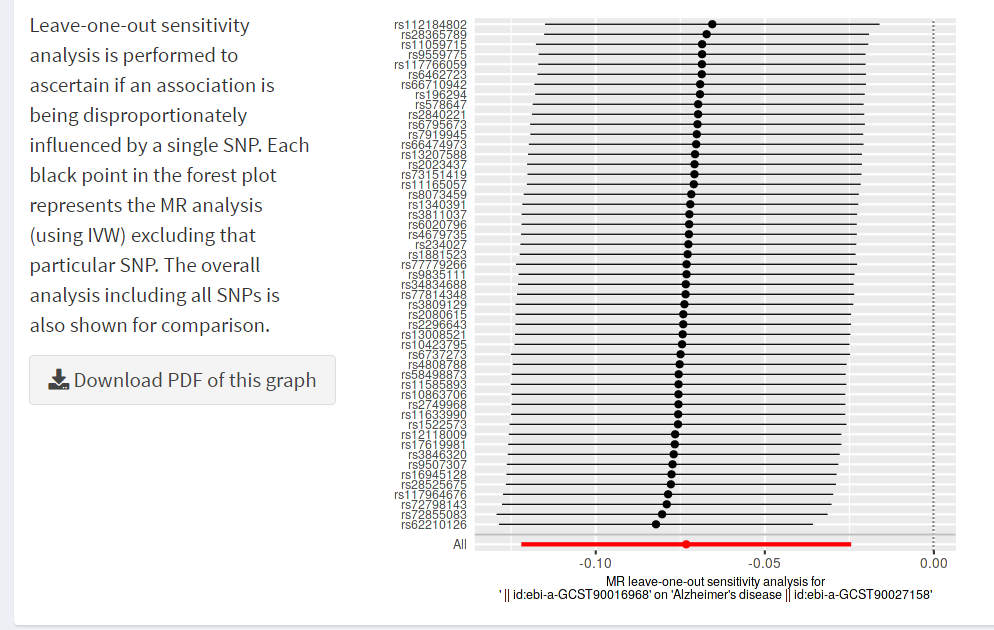
앞선 상관관계 분석값에서의 leave-one-out sensivity analysis 결과값을 보니 특출나게 틔어나온 SNPs는 없어 보입니다.
사실 Twosample MR을 수행할 수 있는 MR base 플랫폼에서 IVW, MR-Egger regression, leave-one-out analysis 모두를 한번에 파악할 수 있게 해주는데 사용해보시면 유용하실 듯합니다.
https://app.mrbase.org/
Mendelian randomization using summary data from genome-wide association studies (GWAS) is an increasingly important tool for appraising causality in hypothesized exposure-outcome pathways. The approach can, however, be technically challenging and time cons
app.mrbase.org
이것으로 졸업논문 관련 배경지식 공부를 마치고, 다시 translation 관련 이론 복습으로 돌아가보도록 하겠습니다.
참고 자료
1) Sanderson E, Glymour MM, Holmes MV, Kang H, Morrison J, Munafò MR, Palmer T, Schooling CM, Wallace C, Zhao Q, Smith GD. Mendelian randomization. Nat Rev Methods Primers. 2:6 (2022).
2) Lee CH, Cook S, Lee JS, Han B. Comparison of Two Meta-Analysis Methods: Inverse-Variance-Weighted Average and Weighted Sum of Z-Scores. Genomics Inform. 14(4):173-180 (2016).
3) Lee, Young Ho. Overview of Mendelian Randomization Analysis. Journal of Rheumatic Diseases. 4;27 2233-4718 (2020)
4) Boehm FJ, Zhou X. Statistical methods for Mendelian randomization in genome-wide association studies: A review. Comput Struct Biotechnol J. 20:2338-2351 (2022).
5) Szumilas M. Explaining odds ratios. J Can Acad Child Adolesc Psychiatry. 2010 Aug;19(3):227-9. Erratum in: J Can Acad Child Adolesc Psychiatry. 24(1):58. (2015).
6) Hemani, G., et.al. The MR-Base platform supports systematic causal inference across the human phenome, eLife, 7, e34408 (2018).




